programme.lv

Dārgākais posms

ļoti grūts

Uzdevums no Latvijas 38. (2024./2025. m.g.) informātikas olimpiādes (LIO) valsts kārtas; vecākajai (11.-12. klašu) grupai.

Stāsts

Loģistika ir zinātne par to, kā jebkuras sistēmas ietvaros objektīvāk plānot, regulēt un kontrolēt informācijas, materiālu, produkcijas, cilvēku un enerģijas plūsmas, kā arī visaptveroša šo plūsmu vadīšana; ar ražojumu izplatīšanu saistīto darbu optimizēšana.

Pētnieks Konrāds šobrīd analizē kādas transporta firmas materiālu pārvadāšanas plūsmas. Viņš ir noskaidrojis, ka firma savus pārvadājumus veic tikai starp noteiktām pilsētām tā, ka katrs posms saista tieši divas pilsētas, turklāt pārvadājums no vienas pilsētas līdz kādai citai vienmēr ir šādu posmu virkne, kas vienmēr iespējama tikai vienā vienīgā veidā. Pilsētas ir sanumurētas ar naturāliem skaitļiem no $1$ līdz $N$ pēc kārtas.

Vienas šādas sistēmas ar pilsētas savienojošajiem posmiem piemērs parādīts 1. attēlā.

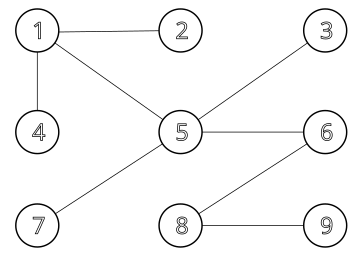
1. attēls: Pilsētas un tās savienojošie posmi (zināmā struktūra)

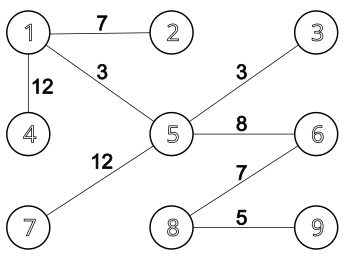
2. attēls: Pilsētas un tās savienojošie posmi (nezināmās posmu izmaksas)

Konrāds ir noskaidrojis, ka pārvadājumu izmaksas katrā posmā var izteikt kā naturālu skaitli, kas nepārsniedz kādu zināmu vērtību $S_m$ , un tās dažādiem posmiem var atšķirties. Viņš vēlas noteikt, kurā posmā izmaksas ir vislielākās. Diemžēl firma nevēlas sniegt pilnu informāciju par esošajām izmaksām, bet ir gatava sniegt atbildi "jā" vai "nē" uz šādiem vaicājumiem: "Vai maršrutā no pilsētas $X$ līdz pilsētai $Y$ kādā posmā pārvadājumu izmaksas ir vismaz $S$ ?"

Uzrakstiet datorprogrammu, kas ģenerē šādu vaicājumu virkni ar mērķi atrast posmu ar vislielākajām pārvadājumu izmaksām!

Komunikācija

Šis ir interaktīvs uzdevums. Jūsu programmai, sākot darbu, pirmajā ievaddatu rindā doti divi naturāli skaitļi $N$ (pilsētu skaits, $2 \leq N \leq 5000$ ) un $S_m$ (maksimālās iespējamās viena posma izmaksas, $S_m \leq 10^9$ ), kas atdalīti ar tukšumzīmi. Nākamajā $N-1$ ievaddatu rindā katrā dots viena divas pilsētas savienojošā posma apraksts -- savienoto pilsētu numuri, kas atdalīti ar tukšumzīmi.

Dārgākā posma (vai posmu) atrašanās vietu un precīzās tā izmaksas vērtēšanas sistēma tur slepenībā.

Tad jūsu programma var veikt vaicājumus, tos rakstot izvadā sekojošā formātā: "0 $p_1$ $p_2$ $s$ ", kur $p_1$ un $p_2$ ir divu pilsētu numuri -- atšķirīgi naturāli skaitļi $(1 \leq p_1, p_2 \leq N)$ , bet $s$ $(1 \leq s \leq S_m)$ -- izmaksas, izteiktas kā naturāls skaitlis. Vērtēšanas sistēma uz vaicājumu izdod atbildi nākamajā ievaddatu rindā. Atbilde ir vesels skaitlis -- $0$ , ja maršrutā no $p_1$ līdz $p_2$ visu posmu izmaksas ir mazākas par $s$ , vai $1$ , ja vismaz viena posma izmaksas ir lielākas vai vienādas ar $s$ .

Jūsu programma katrā testā var veikt ne vairāk kā $150000$ vaicājumus.

Kad dārgākā posma atrašanās vieta noteikta, programmai jāizvada "1 $p_x$ $p_y$ " ( $1 \leq p_x, p_y \leq N$ ), kur $p_x$ un $p_y$ ir dārgākā posma galos esošo pilsētu numuri, un darbība jābeidz. Vērtēšanas sistēma neatbildēs uz šo izvadu un nepieņems sekojošus vaicājumus.

Ja sistēmā ir vairāki posmi ar dārgākajām izmaksām, jāizvada informācija par jebkuru no tiem. Raksturojot posmu, pilsētu numuru secībai nav nozīmes.

Piemērs

Ievaddati	Izvaddati (Jūsu programmas vaicājumi)	Komentāri
`9 16 2 1 8 9 4 1 1 5 5 6 5 7 8 6 3 5`		Atbilst 1. attēlam.
	`0 2 9 10`
`0`
	`0 4 7 10`
`1`
	`0 7 4 13`
`0`
	`0 7 4 12`
`1`
	`0 5 3 12`
`0`
	`0 4 1 12`
`1`
	`1 1 4`	Visdārgākais posms ir starp $1$ un $4$ . Tikpat dārgs, bet ne dārgāks, pēc šī dialoga rezultātiem var būt posms starp $5$ un $7$ .

Izpildes resursu ierobežojumi

CPU izpildes laiks uz testu: 1.5 sekundes.

RAM atmiņas apjoms uz testu: 256 megabaiti.

Apakšuzdevumi un to vērtēšana

#	Apakšuzdevuma apraksts	Punkti
1.	Kreisās pilsētas skaits ir 2.	1
2.	Katrā pilsētā ne vairāk kā 2 savienojumi ar citām pilsētām.	10
3.	Dārgākā posma izmaksas nepārsniedz 2.	10
4.	Dārgākā posma izmaksas nepārsniedz 256.	15
5.	Nav papildu ierobežojumu.	64

Apakšuzdevumu punktu summa = 100.

Ja ir pareizi atrasts bojātais kabelis, tad atkarībā no veikto vaicājumu skaita $Q$ katram testam tiek aprēķināta tā kvalitāte. To aprēķina šādi:

Ja $Q \leq 3500$ , tad "kvalitāte" $= 1$ .
Ja $3500 < Q \leq 10000$ , tad "kvalitāte" $= 1 - (Q - 3500) / 10000$ .
Ja $10000 < Q \leq 50000$ , tad "kvalitāte" $= 0.35 - (Q - 10000) / 400000$
Ja $50000 < Q \leq 150000$ , tad "kvalitāte" $= 0.25 - (Q - 50000) / 500000$
Ja $150000 < Q$ , tad "kvalitāte" $= 0$ .

Ja grupā ir iekļauti vairāki testi, tad grupas vērtējumu nosaka vissliktāk izpildītais tests (kura kvalitāte ir vismazākā). Par testu grupu piešķirto punktu skaitu aprēķina kā: "Piešķirtais punktu skaits" $= \text{Sliktākā testa kvalitāte grupā} \cdot \text{Punktu skaits par grupu}$

Piezīmes

Lai garantētu, ka jūsu programmas "vaicājumus" saņem vērtēšanas sistēma, jums ir "jāsinhronizē" ( flush ) izvaddatu plūsma ( stdout ) pēc katra vaicājuma.

Valoda	Piemērs
C++	`std::cout << something << std::endl;` ... "std::endl" nodrošina sinhronizāciju
Go	`fmt.Println(something)` ... standarta datu plūsma nav īpaši jāsinhronizē
Java	`System.out.println(something); System.out.flush();`
Pascal	`writeln(something); flush(output);`
Python	`print(something, flush=True)`

Ja testa ietvaros tiks pārsniegts maksimāli atļautais vaicājumu skaits, tā statuss pēc testēšanas būs "Nepareiza atbilde".