
Otrais ceļojums

Stāsts
Tūristu iecienītajā Krokodilu salā ir pilsētas, kas numurētas ar naturāliem skaitļiem no līdz pēc kārtas. Visas pilsētas savā starpā savieno ceļu tīkls. Ceļi ir izbūvēti tā, ka no katras pilsētas uz jebkuru citu iespējams aizbraukt pa ceļiem tikai vienā vienīgā veidā. Tūristu ērtībām katrā salas pilsētā ir lidosta, kurā tūristi var sākt un beigt savus ceļojumus. Ceļojumu aģentūra „Jaunie skati” piedāvā organizēt ceļojumus uz Krokodilu salu, kuri noris šādi: vispirms tūrists ar lidmašīnu tiek aizvests uz kādu no Krokodilu salas pilsētām (apzīmēsim to ar ), pēc tam, vadoties no tūrista interesēm, viņš vai viņa vai nu visu ceļojuma laiku pavada šajā pilsētā, vai arī ar automašīnu apmeklē citas pilsētas, nevienu pilsētu neapmeklējot atkārtoti. Ceļojuma beigās no pēdējās apmeklētās pilsētas (apzīmēsim to ar ) tūrists ar lidmašīnu tiek pārvests mājās.
Šobrīd „Jaunie skati” ir sastapušies ar šādu problēmu: vairāki tūristi jau vienreiz ir viesojušies Krokodilu salā un vēlētos to apmeklēt vēlreiz, bet nevēlas apmeklēt otrreiz nevienu no tām pilsētām, kurā jau reiz ir bijuši. Aģentūra katram zināmam tūrista iepriekšējā ceļojuma galapunktiem un vēlas noskaidrot, cik atšķirīgus iepriekš aprakstītā veida ceļojumus šim tūristam tā var piedāvāt. Divi ceļojumi ir atšķirīgi, ja tajos atšķiras vismaz viena apmeklējamā pilsēta. Līdz ar to maršruts, kas piedāvā apmeklēt tās pašas pilsētas pretējā secībā, netiek uzskatīts par atšķirīgu maršrutu.
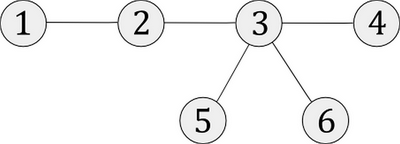
Piemēram, ja ceļu tīkls ir tāds, kā redzams 1. attēlā un pirmajā ceļojumā tūrists ceļojumu sāka pilsētā Nr. 5, bet beidza pilsētā Nr. 4, tad tūrists ir apmeklējis arī pilsētu Nr. 3. Otrajam ceļojumam aģentūra var piedāvāt šādus četrus atšķirīgus ceļojuma maršrutus, kas neietver iepriekš apmeklētās pilsētas (norādīta ceļojuma sākuma un beigu pilsēta): , , un .
Uzrakstiet programmu, kas dotam pirmā ceļojuma aprakstam, aprēķina atšķirīgo otrā ceļojuma veidu skaitu!
Ievaddati
Ievaddatu pirmajā rindā dotas trīs naturālu skaitļu – pilsētu skaits , pirmā ceļojuma sākuma pilsētas numurs un pirmā ceļojuma beigu pilsētas numurs . Katri divi skaitļi ievaddatos atdalīti ar tukšumzīmi.
Katrā no nākamajām ievaddatu rindām dots viena ceļa apraksts – tā galapunkta pilsētu numuri. Katra ceļa apraksts failā dots vienreiz. Katri divi skaitļi ievaddatos atdalīti ar tukšumzīmi.
Izvaddati
Izvaddatu vienīgajā rindā jāizvada vesels nenegatīvs skaitlis – atšķirīgo otrā ceļojuma variantu skaits.
Piemēri
Ievaddati
6 5 4
1 2
3 2
3 4
3 5
6 3
Izvaddati
4
Piezīme:
Atbilst piemēram uzdevuma tekstā.
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Uzdevuma tekstā dotie divi testi | 2 |
| 2. | 5 | |
| 3. | 15 | |
| 4. | 18 | |
| 5. | 24 | |
| 6. | 36 |
1. apakšuzdevuma ievaddati
8 3 3
1 2
2 3
3 4
4 5
6 1
6 7
6 8
15 2 1
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
5 10
5 11
6 12
6 13
7 14
7 15

Otrais ceļojums

Stāsts
Tūristu iecienītajā Krokodilu salā ir pilsētas, kas numurētas ar naturāliem skaitļiem no līdz pēc kārtas. Visas pilsētas savā starpā savieno ceļu tīkls. Ceļi ir izbūvēti tā, ka no katras pilsētas uz jebkuru citu iespējams aizbraukt pa ceļiem tikai vienā vienīgā veidā. Tūristu ērtībām katrā salas pilsētā ir lidosta, kurā tūristi var sākt un beigt savus ceļojumus. Ceļojumu aģentūra „Jaunie skati” piedāvā organizēt ceļojumus uz Krokodilu salu, kuri noris šādi: vispirms tūrists ar lidmašīnu tiek aizvests uz kādu no Krokodilu salas pilsētām (apzīmēsim to ar ), pēc tam, vadoties no tūrista interesēm, viņš vai viņa vai nu visu ceļojuma laiku pavada šajā pilsētā, vai arī ar automašīnu apmeklē citas pilsētas, nevienu pilsētu neapmeklējot atkārtoti. Ceļojuma beigās no pēdējās apmeklētās pilsētas (apzīmēsim to ar ) tūrists ar lidmašīnu tiek pārvests mājās.
Šobrīd „Jaunie skati” ir sastapušies ar šādu problēmu: vairāki tūristi jau vienreiz ir viesojušies Krokodilu salā un vēlētos to apmeklēt vēlreiz, bet nevēlas apmeklēt otrreiz nevienu no tām pilsētām, kurā jau reiz ir bijuši. Aģentūra katram zināmam tūrista iepriekšējā ceļojuma galapunktiem un vēlas noskaidrot, cik atšķirīgus iepriekš aprakstītā veida ceļojumus šim tūristam tā var piedāvāt. Divi ceļojumi ir atšķirīgi, ja tajos atšķiras vismaz viena apmeklējamā pilsēta. Līdz ar to maršruts, kas piedāvā apmeklēt tās pašas pilsētas pretējā secībā, netiek uzskatīts par atšķirīgu maršrutu.
Piemēram, ja ceļu tīkls ir tāds, kā redzams 1. attēlā un pirmajā ceļojumā tūrists ceļojumu sāka pilsētā Nr. 5, bet beidza pilsētā Nr. 4, tad tūrists ir apmeklējis arī pilsētu Nr. 3. Otrajam ceļojumam aģentūra var piedāvāt šādus četrus atšķirīgus ceļojuma maršrutus, kas neietver iepriekš apmeklētās pilsētas (norādīta ceļojuma sākuma un beigu pilsēta): , , un .

Uzrakstiet programmu, kas dotam pirmā ceļojuma aprakstam, aprēķina atšķirīgo otrā ceļojuma veidu skaitu!
Ievaddati
Ievaddatu pirmajā rindā dotas trīs naturālu skaitļu – pilsētu skaits , pirmā ceļojuma sākuma pilsētas numurs un pirmā ceļojuma beigu pilsētas numurs . Katri divi skaitļi ievaddatos atdalīti ar tukšumzīmi.
Katrā no nākamajām ievaddatu rindām dots viena ceļa apraksts – tā galapunkta pilsētu numuri. Katra ceļa apraksts failā dots vienreiz. Katri divi skaitļi ievaddatos atdalīti ar tukšumzīmi.
Izvaddati
Izvaddatu vienīgajā rindā jāizvada vesels nenegatīvs skaitlis – atšķirīgo otrā ceļojuma variantu skaits.
Piemēri
Ievaddati
6 5 4
1 2
3 2
3 4
3 5
6 3
Izvaddati
4
Piezīme:
Atbilst piemēram uzdevuma tekstā.
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Uzdevuma tekstā dotie divi testi | 2 |
| 2. | 5 | |
| 3. | 15 | |
| 4. | 18 | |
| 5. | 24 | |
| 6. | 36 |
1. apakšuzdevuma ievaddati
8 3 3
1 2
2 3
3 4
4 5
6 1
6 7
6 8
15 2 1
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
5 10
5 11
6 12
6 13
7 14
7 15